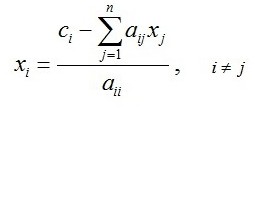Lineer denklem sistemlerinin çözümü için basit yineleme yöntemi (SLAE)

formasyon

Basit yineleme yöntemi, ayrıca yöntem olarak adlandırılırSıralı yaklaşım, bilinmeyen bir miktarın değerini yavaş yavaş inceleyerek bulmak için matematiksel bir algoritmadır. Bu yöntemin özü, adından da anlaşılacağı gibi, ilk yaklaşımdan aşamalı olarak gelişmekte, daha sonrakilere daha fazla rafine sonuçlar elde edilmektedir. Bu yöntem, belirli bir fonksiyondaki bir değişkenin değerini bulmak için olduğu gibi, lineer ve lineer olmayan denklem sistemlerini çözmek için kullanılır.

Bu yöntemin, SLAE'yi çözmede nasıl uygulandığını ele alalım. Basit yineleme yöntemi aşağıdaki algoritmaya sahiptir:

1. Orijinal matriste yakınsama koşulunun yerine getirildiğinin doğrulanması. Yakınsama teoremi: Eğer sistemin başlangıç matrisi diyagonal bir hakimiyete sahipse (yani, her bir çizgide, ana diyagonalin elemanları moduloda yan çapraz elemanların toplamından daha büyük olmalıdır), o zaman basit yineleme yöntemi yakınsaktır.

2. Orijinal sistemin matrisi her zaman çapraz bir baskınlığa sahip değildir. Bu gibi durumlarda, sistem dönüştürülebilir. Yakınsama koşulunu sağlayan denklemler dokunulmadan bırakılır ve tatmin edici olmayan lineer kombinasyonlar ile yapılır, yani. Çarpın, çıkartın, istenilen sonucu elde edene kadar denklemleri birbirine ekleyin.

Eğer ana diyagonalde ortaya çıkan sistemde uygunsuz katsayılar varsa, o zaman bu denklemin her iki parçasına da formun c_ben* x_iişaretler diyagonal elemanların belirtileriyle örtüşmelidir.

3. Elde edilen sistemin normal forma dönüşümü:

x^-= β^-+ α * x^-

Bu, örneğin, aşağıdaki gibi çeşitli şekillerde yapılabilir: ilk denklem ifade x den₁ diğer bilinmeyenler aracılığıyla, ikinci₂üçüncü₃ ve benzeri. Aşağıdaki formülleri kullanıyoruz:

α_ij= - (a_ij/ a_ii)

_ben= b_ben/ a_ii
Ortaya çıkan normal form sisteminin yakınsama durumuna karşılık geldiğini tekrar doğrulamamız gerekir:

Σ (j = 1) | α_ij| ≤ 1, i = 1,2 ile ... n

4. Aslında, ardışık yaklaşım yöntemlerini uygulamaya başlarız.

x⁽⁰⁾- başlangıç yaklaşımı, bunu ifade ediyoruz x⁽¹⁾sonra x ile⁽¹⁾ x ifade ediyoruz⁽²⁾. Matris formundaki genel formül şöyle:

x^(K)= β^-+ α * x^(N-1)

Gerekli doğruluğu elde edene kadar hesaplıyoruz:

max | x_ben(k) -x_ben(k + 1) ≤ ε

Yani, pratikte basit yineleme yöntemini inceleyelim. örnek:
SLAU'yu çözmek için:

4.5x1-1.7x2 + 3.5x3 = 2
3.1x1 + 2.3x2-1.1x3 = 1
1,8x1 + 2,5x2 + 4.7x3 = 4 doğruluk ile ε = 10^-3

Köşegen elemanların modulusda baskın olup olmadığını görelim.

Sadece üçüncü denklemin yakınsama durumunu karşıladığını görüyoruz. Birinci ve ikinci dönüşümü, ikinci denklemi ekliyoruz:

7.6x1 + 0.6x2 + 2.4x3 = 3

Üçüncüsünden ilkini çıkarırız:

-2,7x1 + 4.2x2 + 1.2x3 = 2

Orijinal sistemi eşdeğer bir taneye dönüştürdük:

7.6x1 + 0.6x2 + 2.4x3 = 3
-2,7x1 + 4.2x2 + 1.2x3 = 2
1,8x1 + 2,5x2 + 4,7x3 = 4

Şimdi sistemi normal forma indiriyoruz:

x1 = 0.3947-0.0789x2-0.3158x3
x2 = 0.4762 + 0.6429x1-0.2857x3
x3 = 0.8511-0.383x1-0.5319x2

Yinelemeli sürecin yakınsaklığını kontrol ederiz:

0,0789 + 0,3158 = 0,3947 ≤ 1
0.6429 + 0.2857 = 0.9286 ≤ 1
0.383 + 0.5319 = 0.9149, 1, yani. şart tatmin.

0,3947
İlk yaklaşım x⁽⁰⁾ = 0.4762
0,8511

Bu değerleri normal formun denklemiyle değiştiririz, aşağıdaki değerleri elde ederiz:

0,08835
x⁽¹⁾= 0.486793
0,446639

Yeni değerlerin yerini alırsak,

0,215243
x⁽²⁾= 0.405396
0,558336

Verilen koşulu karşılayan değerlere yaklaştığımız andaki hesaplamalara devam ediyoruz.

0,18813

x⁽⁷⁾= 0.441091

0,544319

0,188002

x⁽⁸⁾= 0.44164

0,544428

Sonuçların doğruluğunu kontrol edelim:

4,5 x 0,1880 -1,7 * 0,441 + 3,5 * 0,544 = 2,0003
3,1 * 0,880 + 2,3 * 0,441-1,1x * 0,544 = 0,9987
1,8 * 0,1880 + 2,5 * 0,441 + 4,7 * 0,544 = 3,9977

İlk denklemlerde bulunan değerlerin yerini alarak elde edilen sonuçlar, denklemin koşullarını tamamen yerine getirir.

Gördüğümüz gibi, basit yineleme yöntemi oldukça doğru sonuçlar verir, ancak bu denklemi çözmek için çok fazla zaman harcamak ve çok fazla hesaplama yapmak zorunda kaldık.